【课程推荐】MCV4U 微积分与向量

在OSSD课程体系中，12年级的数学课程被分为三门主要课程：MHF4U（高级函数）、MCV4U（微积分与向量）和MDM4U（数据管理）。

对于计划在大学学习科学、工程、计算机科学、经济学等相关专业的学生来说，这门课程是必修的基础课程。它不仅为学生提供了基本的微积分知识，还涉及向量的应用，这些都是大学理工科和经济学专业所必需的。

关于MCV4U

课程名称：微积分与向量 Calculus and Vectors

课程代码：MCV4U

课程类别：大学预备课程

课程大纲：以学生已有的函数知识及对变化率的初步理解为基础，进一步拓展学习内容。学生将解决涉及向量几何与代数表征、三维空间中直线与平面表示的问题；将变化率的概念延伸至多项式函数、正弦函数、指数函数、有理函数及根式函数的导数研究；并运用这些概念与技能建立现实世界关系的数学模型。

课程目标：培养逻辑分析和问题解决能力，建立强大的数学基础，提供进入理工科和经济学专业的必备知识，为未来的学术和职业道路做好准备。

学分数量：1

前置课程：MHF4U

教学内容

微积分：

函数的极限与连续性：学习极限的概念和计算，理解连续函数的性质。

导数：掌握导数的定义和应用，包括曲线的切线、物体加速度以及极值问题。

积分：介绍不定积分和定积分及其在计算面积和体积中的应用。

向量：

向量的基本概念：理解向量的定义、表示及运算，如加法、减法和数乘。

向量的几何应用：学习点积和叉积及其物理意义。

向量方程：探讨直线和平面的向量方程及应用。

评分标准与学习目标

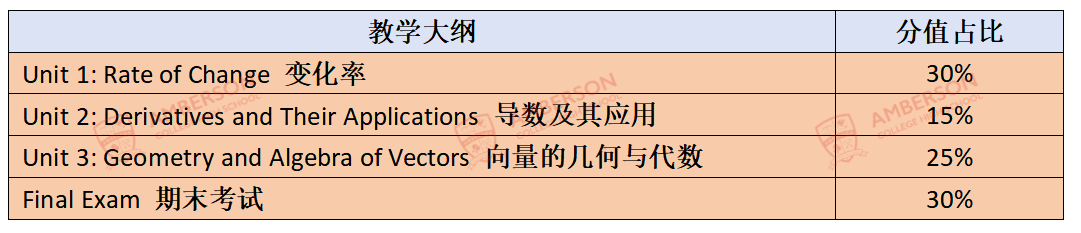
▶评分标准

课程满分100%，平时成绩70% + 期末考试30%

平时成绩70%：三个单元的课后作业和单元测验

▶学生应达到如下目标：

1. 通过建立区间平均变化率与点瞬时变化率的关联，运用割线斜率、切线斜率及极限概念，展现对变化率的理解；

2. 绘制多项式函数、正弦函数及指数函数的导数图像，建立函数及其导数的数值、图像与代数表征之间的关联；

3. 通过图像与代数方法验证求导法则，应用这些法则确定多项式、正弦函数、指数函数、有理函数及根式函数以及简单组合函数的导数，并解决相关问题；

4. 从图像与代数角度，建立函数关键特征与其一阶、二阶导数的关联，并应用于曲线绘制；

5. 运用导数相关概念与方法解决实际问题（包括最优化问题），涉及现实应用场景及数学建模过程；

6. 通过代数与几何表征及实际应用识别，展现对二维与三维空间向量的理解；

7. 对二维与三维空间向量进行运算，利用运算性质解决实际问题（包括现实应用问题）；

8. 区分二维与三维空间中单个线性方程及方程组解的几何表征，确定三维空间中直线与平面的不同几何构型；

9. 运用标量方程、向量方程及参数方程表示直线与平面，解决距离与交点相关问题。